Proposals and Selection
Proposals
The quality of your proposals, 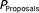 ,
affects the difficulty of and value created by your project selection. To consider
the difficulty of project selection, suppose you have fifty proposals to choose
from. If forty-five of them are Bad proposals, creating a successful portfolio
is difficult. If forty-five of them are Good proposals, even random selection
makes money. ,
affects the difficulty of and value created by your project selection. To consider
the difficulty of project selection, suppose you have fifty proposals to choose
from. If forty-five of them are Bad proposals, creating a successful portfolio
is difficult. If forty-five of them are Good proposals, even random selection
makes money.
Figure 2 illustrates this relationship. The horizontal
axis shows 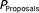 ,
and the vertical axis on the left shows the ,
and the vertical axis on the left shows the 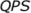 needed to produce
needed to produce 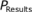 = 80%.
The dark curve shows the relationship. When = 80%.
The dark curve shows the relationship. When 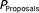 is small, achieving
is small, achieving 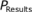 = 80%
requires tremendous skill, which no company can achieve. When = 80%
requires tremendous skill, which no company can achieve. When 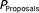 > 40%
the goal becomes attainable, and as > 40%
the goal becomes attainable, and as 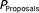 increases further, achieving the goal becomes easy.
increases further, achieving the goal becomes easy.
Now consider how 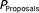 affects portfolio value. In Figure 2 the vertical axis
on the right shows
affects portfolio value. In Figure 2 the vertical axis
on the right shows 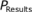 .
The light curve shows how .
The light curve shows how 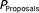 affects
affects 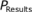 when when 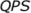 = 3
(a realistic value). Increasing = 3
(a realistic value). Increasing  raises
raises  , which
increases a portfolio's value. , which
increases a portfolio's value.
Figure 2: How the quality of proposals affect project selection and portfolios
Project Selection
Two aspects of PPM affect the quality of your project selection,  .
The first aspect is the quality of your project prioritization. The quality of
your prioritization is affected by uncertainty, the complexity of your proposals
and your evaluation technique. Uncertainty and complexity cause evaluation errors.
They make some Good proposals look like Bad ones, and vice versa. These errors
decrease the quality of prioritization. As uncertainty and complexity increase,
the quality of your prioritization decreases. (We will consider evaluation techniques
later in this paper.) .
The first aspect is the quality of your project prioritization. The quality of
your prioritization is affected by uncertainty, the complexity of your proposals
and your evaluation technique. Uncertainty and complexity cause evaluation errors.
They make some Good proposals look like Bad ones, and vice versa. These errors
decrease the quality of prioritization. As uncertainty and complexity increase,
the quality of your prioritization decreases. (We will consider evaluation techniques
later in this paper.)
While your prioritization is imperfect, it is still useful. The higher a proposal's
evaluation, the more likely the proposal is a Good one. The lower a proposal's
evaluation, the more likely the proposal is a Bad one. This quality of prioritization
causes a second aspect of PPM to affect the quality of your project selection.
Fortunately, this aspect is something you control completely. It is the number
of proposals that you select.
To see how selecting more or fewer proposals affects the quality of project
selection, consider what happens when you fund down a ranking. Suppose you select
cautiously by selecting only the proposals with the highest evaluations. Your
portfolio will be small, but the selected proposals are the most likely ones to
be Good proposals. Your portfolio will have a high 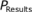 ,
implying that ,
implying that 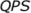 is high as
well. If you select more proposals, these proposals will have poorer evaluations.
They are less likely to be Good ones. As a result, is high as
well. If you select more proposals, these proposals will have poorer evaluations.
They are less likely to be Good ones. As a result, 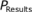 will decrease, which implies a lower value of
will decrease, which implies a lower value of 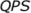 .
The relationship is clear: .
The relationship is clear:
Selecting more proposals reduces the quality of your project
selection.
Because of this relationship, you can adjust the quality of your project selection
by raising or lowering cutoff values, hurdle rates or the sizes of strategic buckets.
(This relationship occurs even when project interactions exist, so long as they
are not too numerous.)
Figure 3 shows the impact of both effects on 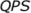 .
Consider the lower curve. If you select all proposals .
Consider the lower curve. If you select all proposals 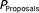 = =  .
This situation implies .
This situation implies  =
1 (see Bayes' law). As you select fewer proposals =
1 (see Bayes' law). As you select fewer proposals 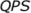 increases. Now consider both curves. The higher curve represents better prioritization.
For all levels of selection, except funding all proposals, it produces a higher
value of
increases. Now consider both curves. The higher curve represents better prioritization.
For all levels of selection, except funding all proposals, it produces a higher
value of 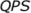 . .
Figure 3: How prioritization & the number of selected proposals affect the
quality of project selection (QPS)
Notice how prioritization and selection interact. Suppose that achieving your
goal for 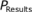 requires
a requires
a 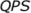 = 2. If your prioritization
is poor, you must select cautiously. If your prioritization is good, you can achieve
your goal while selecting more proposals. By showing how funding down a ranking
affects = 2. If your prioritization
is poor, you must select cautiously. If your prioritization is good, you can achieve
your goal while selecting more proposals. By showing how funding down a ranking
affects 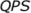 , and thus , and thus 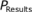 ,
Figure 3 fulfills a need of PPM. It is the first metric
that evaluates project prioritization and shows its impact on the portfolio. ,
Figure 3 fulfills a need of PPM. It is the first metric
that evaluates project prioritization and shows its impact on the portfolio.
|



