Management
Managing Resources
Recall from Figures 4 and 5
that the office laser printer bucket had better proposals and prioritization than
the professional printing bucket. Subsequently, Figures 6
and 7 showed how this advantage produced a better
financial opportunity with laser printers. Based on financial performance, one
should invest more (larger bucket) in laser printers and less (smaller bucket
) in professional printing. Of course, resources also limit investments in opportunities.
By comparing resource constraints to the curves in Figures 6
and 7, you can see if a bucket needs more resources
or if some of its resources should be invested elsewhere.
To allocate resources well, you must also consider the impact of resource allocation
on individual projects. Funding too many projects will spread resources thinly
and cause your projects to suffer. You will turn Good projects into Bad projects
and decrease 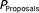 .
(I am grateful to Max Wideman, project management expert and author, for proposing
this mechanism.) .
(I am grateful to Max Wideman, project management expert and author, for proposing
this mechanism.)
The new model can help you solve this problem, but only if your proposal evaluations
consider the adequacy of your resource commitments. Your financial metrics and
decision analysis models should consider multiple resource levels, and your scoring
models should include resource levels as an attribute. If you evaluate proposals
this way, a proposal's score (evaluation) will decrease when your resource allocation
plan reduces its resources.
With this type of evaluation, Figures 8 and 9
will help you assess the impact of your resource allocation on your projects.
As you change the amount of resources dedicated to each project, each project's
score (evaluation) changes. Figure 8 then shows the impact
on each project's chance of success. Derived from your PPM results, Figure 8
provides the probability that a proposal is a Good one, based on its score. Figure 9
shows the probability of success for each project and for 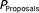 .
The light bars indicate proposals that have a low probability of success because
the current resource allocation plan provides them with inadequate resources.
(By estimating the likelihood of success for each project, Figure 8
can help you assess and manage portfolio risk as well.) .
The light bars indicate proposals that have a low probability of success because
the current resource allocation plan provides them with inadequate resources.
(By estimating the likelihood of success for each project, Figure 8
can help you assess and manage portfolio risk as well.)
Figure 8: Probability of success as a function of project score
Figure 9: Probability of success for each project and 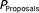
Because resource allocation affects each proposal's probability of success,
resource allocation affects some of the aforementioned metrics. A PPM dashboard
should adjust the metrics so you can see the full impact of your resource allocation
plans. Hopefully, this feedback will eliminate any tendency to fund too many projects.
Managing Phase-Gate Systems
The Bayes' law model shows how Phase-Gate systems behave. Consider the Phase-Gate
system in Figure 10. Selecting more proposals at Gate
1 increases pipeline throughput, but it lowers 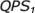 .
A lower .
A lower 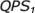 reduces reduces 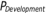 ,
so the pipeline has more downstream failures. Conversely, selecting fewer proposals
at Gate 1 reduces throughput, but it raises ,
so the pipeline has more downstream failures. Conversely, selecting fewer proposals
at Gate 1 reduces throughput, but it raises 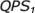 .
A higher .
A higher 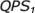 raises raises 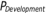 ,
so the pipeline has fewer downstream failures. Downstream failures are more expensive
than upstream failures, thus: ,
so the pipeline has fewer downstream failures. Downstream failures are more expensive
than upstream failures, thus:
Pipeline throughput and ROI are inversely related.
Greater throughput reduces ROI.
Additionally, when 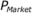 is small, executives are concerned with the consistency of output. Greater throughput
lowers
is small, executives are concerned with the consistency of output. Greater throughput
lowers 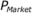 , and from
the theory of geometric distributions, a smaller , and from
the theory of geometric distributions, a smaller 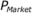 makes a pipeline more volatile. Increasing throughput intensifies booms
and busts.
makes a pipeline more volatile. Increasing throughput intensifies booms
and busts.
Figure 10: The behavior of Phase-Gate systems
These relationships identify the following problems with current pipeline management:
- Selecting projects to maximize NPV at each gate manages each gate independently.
This practice ignores the relationship between upstream project selection and
downstream results.
- Some textbooks and models assume that the gates' attrition rates are independent
of each other. This assumption is wrong.
- Pushing more projects into the front-end increases expensive downstream attrition
while raising pipeline volatility.
- Plans calling for high throughput with high ROI are infeasible and will fail.
The Bayes' law model suggests a new approach to pipeline management. With PPM
results, you estimate 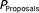 , ,
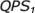 , and if sufficient data
exists, , and if sufficient data
exists, 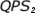 . You then select
the level of throughput that is best for your company. To implement your plan,
raise Gate 1's cutoff value (or hurdle rate) high enough to reduce Gate 2's
attrition to a desired level. Conversely, if Gate 2's attrition rate is too
high, fix the problem by raising Gate 1's cutoff value. By measuring results
downstream and fixing problems upstream, you coordinate project selection throughout
your pipeline. . You then select
the level of throughput that is best for your company. To implement your plan,
raise Gate 1's cutoff value (or hurdle rate) high enough to reduce Gate 2's
attrition to a desired level. Conversely, if Gate 2's attrition rate is too
high, fix the problem by raising Gate 1's cutoff value. By measuring results
downstream and fixing problems upstream, you coordinate project selection throughout
your pipeline.
|



