Definition of the Efficient Frontier
Suppose that an organization is currently conducting a set of projects represented by the point labeled Portfolio A in the graphic shown in Figure 10. Economists would describe Portfolio A as inefficient because there is another project portfolio, Portfolio B that produces more value for the same cost. Similarly, there is also a Portfolio C that produces the same value for less cost. Furthermore, there is a Portfolio D with a combination of these two characteristics.
Figure 10: Different project portfolios have different costs and values
Now suppose we consider all of the alternative project portfolios that can be constructed from a set of project proposals. Typically there are many and Figure 11 shows a real example. In this case the organization had 30 project proposals under consideration in one budget cycle. Four of those projects were considered mandatory (3 process fixes and a new initiative required by regulators) leaving 26 discretionary projects. In general, if there are N potential projects, there are 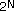 possible project portfolios because there are a total of possible project portfolios because there are a total of 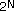 subsets within a set of N items. (For more explanation see the paper Mathematics: Methods for Solving the Capital Allocation Problem, available on my website). Thus, this application required evaluating subsets within a set of N items. (For more explanation see the paper Mathematics: Methods for Solving the Capital Allocation Problem, available on my website). Thus, this application required evaluating 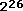 or approximately 67 million portfolios, far more than shown in Figure 11! The best portfolios define the efficient frontier. or approximately 67 million portfolios, far more than shown in Figure 11! The best portfolios define the efficient frontier.
Figure 11: The best project portfolios define the efficient frontier
Notice how the efficient frontier is curved, not straight. This is because the efficient frontier is made up of the best possible projects in the least-cost portfolios, i.e. those portfolios that show up first on the left side of the curve. Such portfolios create the greatest "bang-for-the-buck". As the cost constraint is relaxed and more projects can be added, the new projects are not quite as good as those included earlier. The slope of the curve encompassing these projects is flatter because their bang-for-the-buck is not quite as high. Thus, there is a declining return in the value obtained with each additional increment of cost. This is what causes the curve to transition as shown in Figure 11.
|



